Ello,
When starting my element from any degree over 30, before cresting, the track curves up then down. I'm using quintic and I have it set to -2g. It just inclines before going into the crest. Thanks in advance.
Board index ‹ Roller Coaster Games ‹ No Limits Coaster ‹ Newton 2 bump problem

I have it set at 1G because I'm starting from the lift.
I'm afraid it's the latter. The cosine of 27 degrees is 0.89.
0.891g normal force, 0.454g longitudinal.
You've made 2 mistakes here. First, you've used sine, when you need to use cosine for the normal force (it's not gravity, because gravity is a constant value always directed towards the centre of the earth)
Second, your calculator is set up in radians. It's a very common mistake that I make all the time, you've just go to be vigilant about it.
If you don't know how to convert your calculator to work in degrees (if it's a casio fx-83 or 85, press mode twice then 1) then use the following conversion:
Angle in radians = angle in degrees * pi(or 3.142)/180
(as an aside, radians is a measure of angles that uses the radius of a circle (so 360 degrees = 2*pi, 180 = pi, 1 radian is about 57.3 degrees), it's a lot more efficient way of using rotational speeds distances etc)
If you can't be arsed to do that, here's a quick list of the 5 most popular sines and cosines:
Angle(degrees): 0 - 30 - 45 - 60 - 90
Angle(radians): 0 - pi/6 - pi/4 - pi/3 - pi/2
Cosine(exact): 1 - sqroot(3)/2/2 - 1/sqroot(2) - 0.5 - 0
Cosine(approx): 1 - 0.866 - 0.707 - 0.5 - 0
Sine(exact): 0 - 0.5 - 1/sqroot(2) - sqroot(3)/2 - 1
Sine(approx): 0 - 0.5 - 0.707 - 0.866 - 0
what you did was put your angle in to the calculator in the angular form of miles per hour (i.e. degrees) when the calculator was set up to work with the angles that are easier to work with, but difficult to understand (i.e. radians)
On your calculator screen there will be a little r or a little d somewhere telling you what mode the calculator is operating in. If it's a d, then it's operating in degrees. If it's an r, it's operating in radians.
If you put the wrong type of information in, you'll get the wrong answer, the calculator has no idea if you're doing it wrong or not, it just gets the answer for the information it thinks it's being given.
(I've got no idea of what the newton calculator operates in. put 90 in and the sine should be 1 and the cosine should be 0 if it's in degrees)
Now for the forces, it's difficult to explain without a diagram, and really, you should have been taught this already at school.
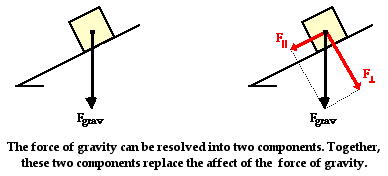 (this is the best I could find)
(this is the best I could find)
Notice, Fgrav points in the same direction, but it can be split up into two components. 1 points parallel to the surface of the hill, and the other points directly down through the track (this is the normal force)
Now, if the angle changes, the gravity force points in the same direction all the time, however the two components change.
If the hill is horizontally flat, i.e. there's no banking. Then there is no force parallel to the track, and the normal force is equal to banking.
If the hill is pointing straight up, i.e. vertical, lift hill angle =90 degrees, then all the force is parallel to the track, and there is no normal force.
If the hill was pointing at a 45 degrees angle, then both forces would be the same.
Now here's where it gets tricky, and the sines and cosines come in. Make sure you understand all of the above before you read the next bit.
what those three forces are actually making is a right angled triangle, with the force of gravity acting as a hypotenuse (i.e. the longest side)
Because it's a right angled triangle, we can use sine and cosine ratios to figure out the size of these parallel and perpendicular forces.
now for the normal force, the angle between it, and the hypotenuse (i.e. Fgrav) is the same as the lift hill angle. We'll call this the adjacent side of the triangle (for reasons that when you do some proper maths, you see)
The cos ratio is equal to the following:
Cos(angle)=adjacent / hypotenuse
now, because we know that the hypoteneuse is equal to 1 g, that simpfies things to this:
Cos(lift hill angle) = Normal force
Now, sin comes into it, because the longtudinal force completes the triangle if it moved so that the start point is at the end of the normal force. Now it is opposite the angle. And the sine ratio is as follows:
sin(angle)=opposite / hypotenuse
which simplifies to:
Sin(lift hill angle) = Longitudinal force
right, now here's a quick check:
what's the normal force of a lift hill at the following angles?
1) 35 degrees a) 0.574 b) 0.819 c) -0.428 d) -0.904
2) 67 degrees a) 0.921 b) 0.391 c) -0.856 d) -0.518
get a calculator and try it. If you get an answer other than b for both, you've done something wrong. And I've chosen the other answers for particular errors that you might make.
Possibly, but he had made a double error. (using sin, and using radians)
nope, engineering student. I do know what I'm talking about though, even though entropy is far smarter (how he can handle quarternions when I could barely get my head around euler the other week I don't know) although newton seems to be crap at letting me do an immelman.
cos it's late, and I couldn't care less about crap like that. Ya happy?
There's a lot of really damn picky people on this board. If I was posting 3 separate statements, then maybe I could slightly understand, but it's the love quote function, it creates a new post automatically. I'm also addressing 3 different people, it makes it easier to read the thread.
Newton 2 bump problem
20 posts
• Page 1 of 1
Just keep scrolling...
It's kind of hard to understand what you mean. Pictures would definitly help.
Just out of curiosity what is the G-force entering the element?
Just out of curiosity what is the G-force entering the element?

I have it set at 1G because I'm starting from the lift.
Just keep scrolling...
You shouldn't set it a 1g because you're starting at a 30 degree angle. 0.866g is the value you need.
Oh. I don't see why though? (Not meant argumentatively)
Just keep scrolling...
Because that's the force pushing riders down into their seat at the given 30* slope. Use the formula (I believe I'm remembering this correctly) cos(theta*degrees) to get the correct normal force, then go from there.
Newton2 should give you the right force if you're coming off a straight segment though, so if that's the case a large segment size when exporting could cause the same problem on small transitions.
Newton2 should give you the right force if you're coming off a straight segment though, so if that's the case a large segment size when exporting could cause the same problem on small transitions.
aye, with a lift hill angle, gravity works normal and longitudinally to the track. It is wholly normal to the ground.
so you have 0.866g normal to the trck and 0.5 g up the track. (I know that's more than one, but if you square them, then add them, they'll equal one.
normal = cos(lift hill angle)*1
longitudinal = sin(lift hill angle)*1
(the times 1 is for the gravity force.) This is only for steady state conditions mind (constant speed or stationary)
so you have 0.866g normal to the trck and 0.5 g up the track. (I know that's more than one, but if you square them, then add them, they'll equal one.
normal = cos(lift hill angle)*1
longitudinal = sin(lift hill angle)*1
(the times 1 is for the gravity force.) This is only for steady state conditions mind (constant speed or stationary)
Ah. Thanks guys.
Just keep scrolling...
I just want to add that if you don't create the lift hill in newton (which as dcs221 pointed out will handle the math for you), newton has a little built in calculator you can use to find the cosine of the angle.
I made the lift hill in the editor then took it from the crest in Newton. I guess I'll just have to deal for this one ride.
Just keep scrolling...
I know I can just use calculators but I wish I payed more attention in geometry
What are these for?
^Same here. What would the gravity be for a 27 degree lift? I got .95637
Is this correct or am I doing yet another thing wrong? haha
Is this correct or am I doing yet another thing wrong? haha
Just keep scrolling...
Originally posted by griffonluv
^Same here. What would the gravity be for a 27 degree lift? I got .95637
Is this correct or am I doing yet another thing wrong? haha
^Same here. What would the gravity be for a 27 degree lift? I got .95637
Is this correct or am I doing yet another thing wrong? haha
I'm afraid it's the latter. The cosine of 27 degrees is 0.89.
Originally posted by griffonluv
^Same here. What would the gravity be for a 27 degree lift? I got .95637
Is this correct or am I doing yet another thing wrong? haha
^Same here. What would the gravity be for a 27 degree lift? I got .95637
Is this correct or am I doing yet another thing wrong? haha
0.891g normal force, 0.454g longitudinal.
You've made 2 mistakes here. First, you've used sine, when you need to use cosine for the normal force (it's not gravity, because gravity is a constant value always directed towards the centre of the earth)
Second, your calculator is set up in radians. It's a very common mistake that I make all the time, you've just go to be vigilant about it.
If you don't know how to convert your calculator to work in degrees (if it's a casio fx-83 or 85, press mode twice then 1) then use the following conversion:
Angle in radians = angle in degrees * pi(or 3.142)/180
(as an aside, radians is a measure of angles that uses the radius of a circle (so 360 degrees = 2*pi, 180 = pi, 1 radian is about 57.3 degrees), it's a lot more efficient way of using rotational speeds distances etc)
If you can't be arsed to do that, here's a quick list of the 5 most popular sines and cosines:
Angle(degrees): 0 - 30 - 45 - 60 - 90
Angle(radians): 0 - pi/6 - pi/4 - pi/3 - pi/2
Cosine(exact): 1 - sqroot(3)/2/2 - 1/sqroot(2) - 0.5 - 0
Cosine(approx): 1 - 0.866 - 0.707 - 0.5 - 0
Sine(exact): 0 - 0.5 - 1/sqroot(2) - sqroot(3)/2 - 1
Sine(approx): 0 - 0.5 - 0.707 - 0.866 - 0
Damn. I'm very confused by all of this...
Just keep scrolling...
Theres alot of teachers on this website.
I think blythy made it sound much more complicated than it is. All you do is take the cosine of the lift angle. You don't even need a calculator, or have to worry about whether your calculator is in the right mode. In newton, just click the button with double arrows to bring up the conversions panel, enter "27" into the text field marked "degrees", and read the cosine right off.

Originally posted by griffonluv
Damn. I'm very confused by all of this...
Damn. I'm very confused by all of this...
what you did was put your angle in to the calculator in the angular form of miles per hour (i.e. degrees) when the calculator was set up to work with the angles that are easier to work with, but difficult to understand (i.e. radians)
On your calculator screen there will be a little r or a little d somewhere telling you what mode the calculator is operating in. If it's a d, then it's operating in degrees. If it's an r, it's operating in radians.
If you put the wrong type of information in, you'll get the wrong answer, the calculator has no idea if you're doing it wrong or not, it just gets the answer for the information it thinks it's being given.
(I've got no idea of what the newton calculator operates in. put 90 in and the sine should be 1 and the cosine should be 0 if it's in degrees)
Now for the forces, it's difficult to explain without a diagram, and really, you should have been taught this already at school.
 (this is the best I could find)
(this is the best I could find)Notice, Fgrav points in the same direction, but it can be split up into two components. 1 points parallel to the surface of the hill, and the other points directly down through the track (this is the normal force)
Now, if the angle changes, the gravity force points in the same direction all the time, however the two components change.
If the hill is horizontally flat, i.e. there's no banking. Then there is no force parallel to the track, and the normal force is equal to banking.
If the hill is pointing straight up, i.e. vertical, lift hill angle =90 degrees, then all the force is parallel to the track, and there is no normal force.
If the hill was pointing at a 45 degrees angle, then both forces would be the same.
Now here's where it gets tricky, and the sines and cosines come in. Make sure you understand all of the above before you read the next bit.
what those three forces are actually making is a right angled triangle, with the force of gravity acting as a hypotenuse (i.e. the longest side)
Because it's a right angled triangle, we can use sine and cosine ratios to figure out the size of these parallel and perpendicular forces.
now for the normal force, the angle between it, and the hypotenuse (i.e. Fgrav) is the same as the lift hill angle. We'll call this the adjacent side of the triangle (for reasons that when you do some proper maths, you see)
The cos ratio is equal to the following:
Cos(angle)=adjacent / hypotenuse
now, because we know that the hypoteneuse is equal to 1 g, that simpfies things to this:
Cos(lift hill angle) = Normal force
Now, sin comes into it, because the longtudinal force completes the triangle if it moved so that the start point is at the end of the normal force. Now it is opposite the angle. And the sine ratio is as follows:
sin(angle)=opposite / hypotenuse
which simplifies to:
Sin(lift hill angle) = Longitudinal force
right, now here's a quick check:
what's the normal force of a lift hill at the following angles?
1) 35 degrees a) 0.574 b) 0.819 c) -0.428 d) -0.904
2) 67 degrees a) 0.921 b) 0.391 c) -0.856 d) -0.518
get a calculator and try it. If you get an answer other than b for both, you've done something wrong. And I've chosen the other answers for particular errors that you might make.
Originally posted by entropy
I think blythy made it sound much more complicated than it is.
I think blythy made it sound much more complicated than it is.
Possibly, but he had made a double error. (using sin, and using radians)
Originally posted by Panther16
Theres alot of teachers on this website.
Theres alot of teachers on this website.
nope, engineering student. I do know what I'm talking about though, even though entropy is far smarter (how he can handle quarternions when I could barely get my head around euler the other week I don't know) although newton seems to be crap at letting me do an immelman.
^ why are you triple posting?
Boulder Dash was the only good roller coaster.
"or if you're when the hydraulic fluid was dumped out of the motor is goes 200ft up the tower and is like "LOL nope"" - CKMWM 2016
"or if you're when the hydraulic fluid was dumped out of the motor is goes 200ft up the tower and is like "LOL nope"" - CKMWM 2016
Originally posted by slosprint
^ why are you triple posting?
^ why are you triple posting?
cos it's late, and I couldn't care less about crap like that. Ya happy?
There's a lot of really damn picky people on this board. If I was posting 3 separate statements, then maybe I could slightly understand, but it's the love quote function, it creates a new post automatically. I'm also addressing 3 different people, it makes it easier to read the thread.
20 posts
• Page 1 of 1
-
- Related topics
- Replies
- Views
- Last post
-
- A problem with Newton 2...
by Tanks4me » June 23rd, 2010, 11:57 am - 3 Replies
- 685 Views
- Last post by devilsrule911
June 23rd, 2010, 3:04 pm
- A problem with Newton 2...
-
- Problem with Newton 2
by Generalcamo » March 20th, 2011, 3:51 pm - 8 Replies
- 978 Views
- Last post by Generalcamo
March 20th, 2011, 7:07 pm
- Problem with Newton 2
-
- Bump Mapping
by AyTrane » July 24th, 2009, 7:39 pm - 0 Replies
- 509 Views
- Last post by AyTrane
July 24th, 2009, 7:39 pm
- Bump Mapping
-
- Newton
by elementz_X » June 7th, 2009, 8:19 pm - 3 Replies
- 1256 Views
- Last post by griffonluv
June 7th, 2009, 8:40 pm
- Newton
-
- Newton 2 Help!
by BirdNerd » October 7th, 2009, 7:40 am - 3 Replies
- 1252 Views
- Last post by BirdNerd
October 7th, 2009, 11:47 am
- Newton 2 Help!


